Honing math skills is tough, let alone teaching it. Or maybe that’s just me, as someone who always slacked off on math problems as a student.
But if there’s one way to tone down the intimidation of blocks of numbers, it’s through math word problems. These turn nauseating equations into relatable, solvable scenarios, making math feel more like a challenge to accomplish instead of slogging through heaps of step-by-step formulae.
In this blog, we’re running down over 100 math word problems across different categories, designed for grades K–12.
And the best part? You can download the entire set as a separate PDF file, so you can easily save, print, or share it with your students (or even use it for yourself!).
How to AI-Generate Accurate Math Word Problems
Alright, hold your horses. We’re getting to the list in a bit. But before we dive in, I’ve got a bonus takeaway hack that you’re going to love.
With the rise of AI tools in education, it’s no surprise that subject-specific expertise, like math, has gotten a major upgrade. While there’s a stereotype that AI struggles with math, one tool stands out as an exception: Edcafe AI .
Edcafe AI, primarily designed for educators, lets you create math word problems on the spot with just a little prompt engineering, and it’s guided by fillable fields it doable, even by AI beginners.
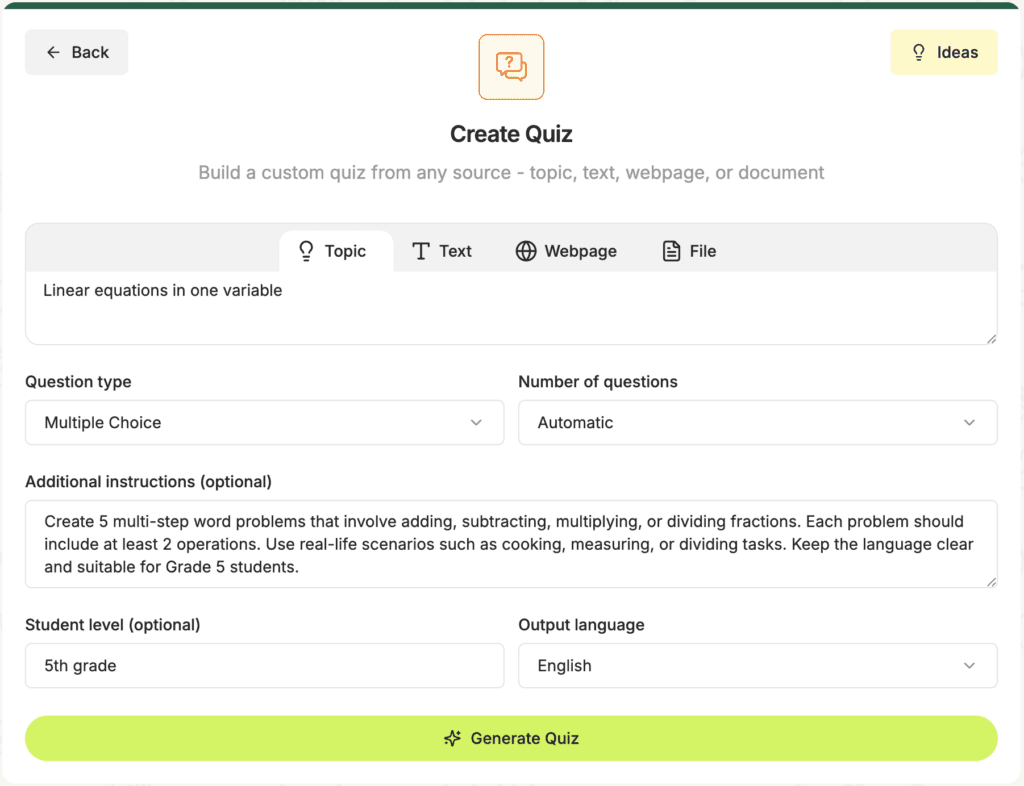
But that’s not all. Beyond creation, Edcafe AI makes math interactive. You can generate a QR code for any problem set, which students can scan to work on the problems directly from their devices, even asynchronously.
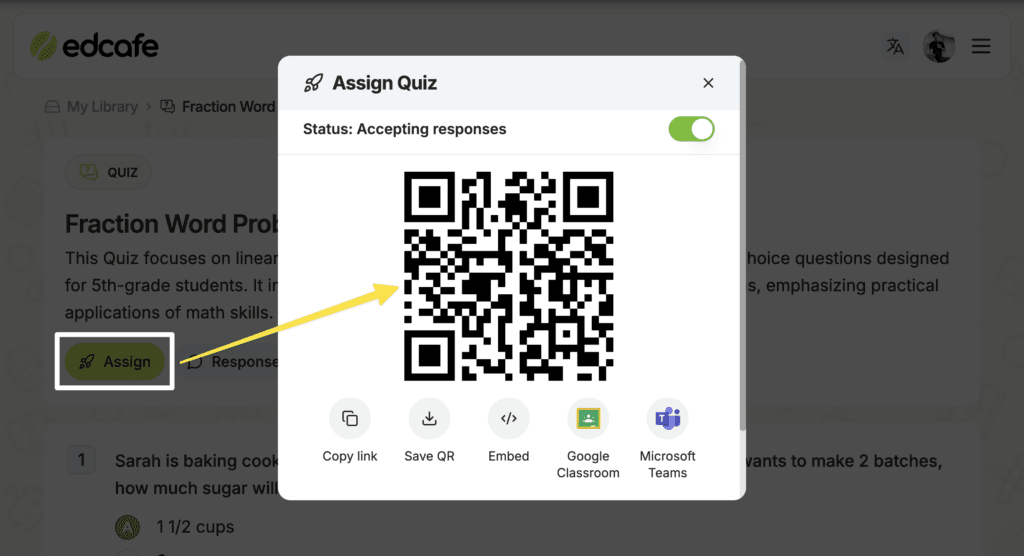
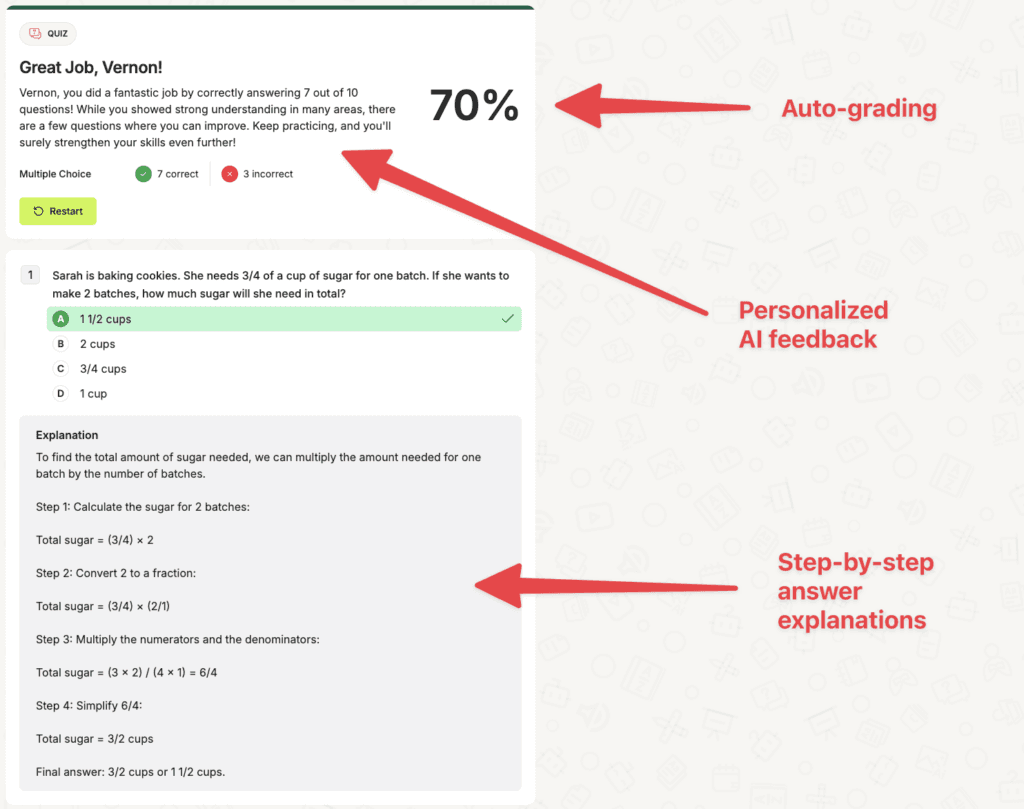
And really, what good is an AI if it can’t be a full teacher extensifon? Edcafe AI also provides spot-on feedback, grading, and step-by-step explanations for each answer.
Counting & Basic Operations (Math Word Problems 1-10)
Best for: Building foundational skills in counting, addition, subtraction, multiplication, and division.
Grades: K–2
Math Problem 1: A farmer plants carrots in rows. If each row contains 5 carrots and there are 6 rows, how many carrots has the farmer planted in total?
✨Solution: Multiply the number of carrots per row by the number of rows: 5 × 6 = 30. The farmer has planted 30 carrots in total.
Math Problem 2: Lila collects seashells on the beach. She finds 8 shells in the morning and 12 more in the afternoon. How many shells does she have at the end of the day?
✨Solution: Add the shells collected: 8 + 12 = 20. Lila has 20 seashells at the end of the day.
Math Problem 3: A school bus has 4 rows of seats, with 3 students sitting in each row. How many students are on the bus?
✨Solution: Multiply the number of rows by the number of students per row: 4 × 3 = 12. There are 12 students on the bus.
Math Problem 4: A puppy has 4 legs, and a bird has 2 legs. If there are 3 puppies and 2 birds, how many legs are there in total?
✨Solution: Multiply and add: (4 × 3) + (2 × 2) = 12 + 4 = 16. There are 16 legs in total.
Math Problem 5: A jar contains 15 candies. If 6 candies are eaten, how many candies remain?
✨Solution: Subtract: 15 − 6 = 9. There are 9 candies remaining.
Math Problem 6: A box holds 8 crayons. If you have 3 boxes, how many crayons do you have in total?
✨Solution: Multiply: 8 × 3 = 24. You have 24 crayons in total.
Math Problem 7: A farmer collects 10 eggs from chickens and 5 eggs from ducks. How many eggs does the farmer collect altogether?
✨Solution: Add: 10 + 5 = 15. The farmer collects 15 eggs.
Math Problem 8: A child builds a tower using 9 blocks. If 4 blocks fall off, how many blocks are left in the tower?
✨Solution: Subtract: 9 − 4 = 5. There are 5 blocks left.
Math Problem 9: A garden has 6 rows of flowers, with 7 flowers in each row. How many flowers are in the garden?
✨Solution: Multiply: 6 × 7 = 42. There are 42 flowers in the garden.
Math Problem 10: A teacher gives 3 stickers to each of her 5 students. How many stickers does she give out in total?
✨Solution: Multiply: 3 × 5 = 15. She gives out 15 stickers in total.
Measurement & Time (Math Word Problems 11-20)
Best for: Understanding real-world applications of measurement and time.
Grades: 1–3
Math Problem 11: A pencil is 15 centimeters long, and a ruler is 30 centimeters long. How much longer is the ruler than the pencil?
✨Solution: Subtract: 30 − 15 = 15. The ruler is 15 centimeters longer.
Math Problem 12: A movie starts at 2:15 PM and ends at 3:45 PM. How long is the movie?
✨Solution: From 2:15 to 3:15 is 1 hour, and from 3:15 to 3:45 is 30 minutes. The movie is 1 hour and 30 minutes long.
Math Problem 13: A jug can hold 2 liters of water. If you fill it halfway, how much water is in the jug?
✨Solution: Divide the capacity by 2: 2 ÷ 2 = 1. The jug contains 1 liter of water.
Math Problem 14: A recipe calls for 2 cups of flour and 1 cup of sugar. If you double the recipe, how many cups of ingredients will you need in total?
✨Solution: Double each ingredient: 2 × 2 = 4 cups of flour and 1 × 2 = 2 cups of sugar. Add them: 4 + 2 = 6. You’ll need 6 cups of ingredients.
Math Problem 15: A train leaves the station at 8:00 AM and arrives at 11:30 AM. How long is the journey?
✨Solution: From 8:00 to 11:00 is 3 hours, and from 11:00 to 11:30 is 30 minutes. The journey is 3 hours and 30 minutes long.
Math Problem 16: A ribbon is 12 meters long. If you cut it into 4 equal pieces, how long is each piece?
✨Solution: Divide the total length: 12 ÷ 4 = 3. Each piece is 3 meters long.
Math Problem 17: A clock shows 4:45 PM. What time will it be 30 minutes later?
✨Solution: Add 30 minutes: 4:45 + 0:30 = 5:15. The time will be 5:15 PM.
Math Problem 18: A bag of rice weighs 5 kilograms. If you use 2 kilograms to cook dinner, how much rice is left?
✨Solution: Subtract: 5 − 2 = 3. There are 3 kilograms of rice left.
Math Problem 19: A pool is filled with 500 liters of water. If 200 liters evaporate, how much water remains?
✨Solution: Subtract: 500 − 200 = 300. There are 300 liters of water remaining.
Math Problem 20: A race track is 400 meters long. If a runner completes 3 laps, how far does the runner go in total?
✨Solution: Multiply: 400 × 3 = 1200. The runner covers 1200 meters.
Patterns & Logical Thinking (Math Word Problems 21-30)
Best for: Developing critical thinking and recognizing patterns.
Grades: 2–4
Math Problem 21: A sequence begins with 2, 4, 6, 8. What is the next number in the sequence?
✨Solution: The pattern increases by 2 each time: 8 + 2 = 10. The next number is 10.
Math Problem 22: If all cats are animals and Fluffy is a cat, is Fluffy an animal?
✨Solution: Yes, because if all cats are animals, and Fluffy is a cat, then Fluffy must also be an animal.
Math Problem 23: A pattern alternates between stars and circles: ★ ○ ★ ○ ★. What comes next in the pattern?
✨Solution: The pattern alternates, so after ★ comes ○. The next symbol is ○.
Math Problem 24: A group of friends stands in a line. If Anna is 3rd in line and Ben is 7th, how many people are between Anna and Ben?
✨Solution: Subtract the positions and subtract 1: 7 − 3 − 1 = 3. There are 3 people between Anna and Ben.
Math Problem 25: A number is greater than 10 but less than 12. What is the number?
✨Solution: The only number greater than 10 but less than 12 is 11.
Math Problem 26: A farmer plants trees in rows. If the first row has 1 tree, the second row has 3 trees, and the third row has 5 trees, how many trees are in the fourth row?
✨Solution: The pattern increases by 2: 5 + 2 = 7. The fourth row has 7 trees.
Math Problem 27: If Monday is the first day of the week, what is the third day?
✨Solution: Count forward from Monday: Tuesday is the second day, and Wednesday is the third. The third day is Wednesday.
Math Problem 28: A puzzle has 5 pieces. If 2 pieces are missing, how many pieces are still in the box?
✨Solution: Subtract: 5 − 2 = 3. There are 3 pieces still in the box.
Math Problem 29: A staircase has steps numbered 1, 2, 3, …, up to 10. If you skip every other step starting from 1, which steps do you land on?
✨Solution: Skip every other step: 1, 3, 5, 7, 9. You land on steps 1, 3, 5, 7, and 9.
Math Problem 30: A sequence of shapes repeats as follows: ▲ ■ ● ▲ ■ ●. What shape comes after ●?
✨Solution: The pattern repeats, so after ● comes ▲. The next shape is ▲.
Fractions & Decimals (Math Word Problems 31-40)
Best for: Introducing fractional thinking and decimal operations.
Grades: 3–5
Math Problem 31: A pizza is cut into 8 equal slices. If you eat 3 slices, what fraction of the pizza have you eaten?
✨Solution: The fraction of the pizza eaten is 3/8. You have eaten three-eighths of the pizza.
Math Problem 32: A water tank is filled to 3/4 of its capacity. If the tank can hold 20 liters when full, how many liters of water are in the tank now?
✨Solution: Multiply the total capacity by 3/4: 20 × 3/4 = 15. There are 15 liters of water in the tank.
Math Problem 33: A recipe calls for 0.75 cups of sugar. If you double the recipe, how much sugar will you need?
✨Solution: Multiply 0.75 by 2: 0.75 × 2 = 1.5. You will need 1.5 cups of sugar.
Math Problem 34: A ribbon is 12 meters long. If you cut off 1/3 of the ribbon, how long is the piece you cut off?
✨Solution: Multiply the total length by 1/3: 12 × 1/3 = 4. The piece you cut off is 4 meters long.
Math Problem 35: A store sells apples for $0.45 each. How much will 8 apples cost?
✨Solution: Multiply the price per apple by the number of apples: 0.45 × 8 = 3.60. The cost is $3.60.
Math Problem 36: A group of friends shares a cake equally. If there are 5 friends, what fraction of the cake does each person get?
✨Solution: Divide the cake into 5 equal parts: 1/5. Each person gets one-fifth of the cake.
Math Problem 37: A book has 120 pages. If you read 1/4 of the book, how many pages have you read?
✨Solution: Multiply the total pages by 1/4: 120 × 1/4 = 30. You have read 30 pages.
Math Problem 38: A runner completes 0.6 of a 10-kilometer race. How far has the runner gone?
✨Solution: Multiply the total distance by 0.6: 10 × 0.6 = 6. The runner has gone 6 kilometers.
Math Problem 39: A bag contains 2/5 kilograms of flour. If you add 3/5 kilograms more, how much flour is in the bag now?
✨Solution: Add the fractions: 2/5 + 3/5 = 5/5 = 1. There is 1 kilogram of flour in the bag.
Math Problem 40: A toy costs $12.50. If you pay with a $20 bill, how much change will you receive?
✨Solution: Subtract the cost from the amount paid: 20 − 12.50 = 7.50. You will receive $7.50 in change.
Geometry & Spatial Reasoning (Math Word Problems 41-50)
Best for: Visualizing shapes, angles, and spatial relationships.
Grades: 4–6
Math Problem 41: A rectangular garden is 10 meters long and 5 meters wide. What is the area of the garden?
✨Solution: Multiply the length by the width: 10 × 5 = 50. The area is 50 square meters.
Math Problem 42: A triangle has a base of 6 centimeters and a height of 4 centimeters. What is the area of the triangle?
✨Solution: Use the formula for the area of a triangle: 1/2 × base × height = 1/2 × 6 × 4 = 12. The area is 12 square centimeters.
Math Problem 43: A square has sides that are 7 centimeters long. What is the perimeter of the square?
✨Solution: Multiply the side length by 4: 7 × 4 = 28. The perimeter is 28 centimeters.
Math Problem 44: A circle has a radius of 5 meters. What is the diameter of the circle?
✨Solution: Multiply the radius by 2: 5 × 2 = 10. The diameter is 10 meters.
Math Problem 45: A rectangular room measures 8 meters by 6 meters. If you want to put a carpet that covers the entire floor, how much carpet do you need?
✨Solution: Multiply the length by the width: 8 × 6 = 48. You need 48 square meters of carpet.
Math Problem 46: A cube has edges that are 3 centimeters long. What is the volume of the cube?
✨Solution: Multiply the edge length three times: 3 × 3 × 3 = 27. The volume is 27 cubic centimeters.
Math Problem 47: A trapezoid has bases of 8 meters and 12 meters, and a height of 5 meters. What is the area of the trapezoid?
✨Solution: Use the formula for the area of a trapezoid: 1/2 × (Base₁ + Base₂) × Height = 1/2 × (8 + 12) × 5 = 50. The area is 50 square meters.
Math Problem 48: A hexagon has 6 sides of equal length. If each side is 4 centimeters long, what is the perimeter of the hexagon?
✨Solution: Multiply the side length by 6: 4 × 6 = 24. The perimeter is 24 centimeters.
Math Problem 49: A rectangle has an area of 36 square meters. If the length is 9 meters, what is the width?
✨Solution: Divide the area by the length: 36 ÷ 9 = 4. The width is 4 meters.
Math Problem 50: A right triangle has one angle measuring 30 degrees. What is the measure of the third angle?
✨Solution: The sum of the angles in a triangle is 180 degrees. Subtract the right angle (90 degrees) and the given angle (30 degrees): 180 − 90 − 30 = 60. The third angle is 60 degrees.
Ratios, Proportions, & Percentages (Math Word Problems 51-60)
Best for: Applying proportional reasoning to everyday situations.
Grades: 5–7
Math Problem 51: The ratio of boys to girls in a class is 3:2. If there are 15 boys, how many girls are there?
✨Solution: Set up a proportion: 3/2 = 15/x. Solve for x: x = 15 × 2 ÷ 3 = 10. There are 10 girls.
Math Problem 52: A shirt costs $20, and there is a 25% discount on the shirt. What is the final price of the shirt after applying the discount?
✨Solution: Calculate the discount: 20 × 0.25 = 5. Subtract the discount from the original price: 20 − 5 = 15. The shirt costs $15 after the discount.
Math Problem 53: A recipe calls for 4 cups of flour to make 16 cookies. How many cups of flour are needed to make 48 cookies?
✨Solution: Set up a proportion: 4/16 = x/48. Solve for x: x = 4 × 48 ÷ 16 = 12. You need 12 cups of flour.
Math Problem 54: A car travels 60 miles in 2 hours. At the same speed, how far will it travel in 5 hours?
✨Solution: Find the speed: 60 ÷ 2 = 30 miles per hour. Multiply by 5: 30 × 5 = 150. The car will travel 150 miles.
Math Problem 55: A bag contains red and blue marbles in a ratio of 5:3. If there are 40 marbles in total, how many are red?
✨Solution: Divide the total into parts: 5 + 3 = 8. Each part is 40 ÷ 8 = 5. Red marbles: 5 × 5 = 25. There are 25 red marbles.
Math Problem 56: A school has 480 students. If 60% of the students are girls, how many girls are there?
✨Solution: Calculate 60% of 480: 480 × 0.60 = 288. There are 288 girls.
Math Problem 57: A map uses a scale of 1 inch = 10 miles. If two cities are 3 inches apart on the map, how far are they in reality?
✨Solution: Multiply the map distance by the scale: 3 × 10 = 30. The cities are 30 miles apart.
Math Problem 58: A mixture contains water and juice in a ratio of 2:3. If there are 10 liters of water, how many liters of juice are there?
✨Solution: Set up a proportion: 2/3 = 10/x. Solve for x: x = 10 × 3 ÷ 2 = 15. There are 15 liters of juice.
Math Problem 59: A store marks up the price of a product by 20%. If the cost price is $50, what is the selling price?
✨Solution: Calculate the markup: 50 × 0.20 = 10. Add the markup to the cost price: 50 + 10 = 60. The selling price is $60.
Math Problem 60: A survey shows that 3 out of every 5 people prefer tea over coffee. If 100 people were surveyed, how many preferred tea?
✨Solution: Calculate the number of tea lovers: 3/5 × 100 = 60. 60 people prefer tea.
Algebraic Thinking (Math Word Problems 61-70)
Best for: Solving for unknowns and understanding variables.
Grades: 6–8
Math Problem 61: Solve for x: 3x + 5 = 14
✨Solution: Subtract 5 from both sides: 3x = 9. Divide by 3: x = 3. The solution is x = 3.
Math Problem 62: A number is tripled and then increased by 7 to give 25. What is the number?
✨Solution: Let the number be x. Write the equation: 3x + 7 = 25. Subtract 7: 3x = 18. Divide by 3: x = 6. The number is 6.
Math Problem 63: If y = 2x + 3, what is y when x = 4?
✨Solution: Substitute x = 4 into the equation: y = 2(4) + 3 = 8 + 3 = 11. The value of y is 11.
Math Problem 64: Two numbers add up to 20, and their difference is 4. What are the two numbers?
✨Solution: Let the numbers be x and y. Write the equations: x + y = 20 and x − y = 4. Add the equations: 2x = 24, so x = 12. Substitute x = 12 into x + y = 20: 12 + y = 20, so y = 8. The numbers are 12 and 8.
Math Problem 65: Solve for x: x/2 − 3 = 7
✨Solution: Add 3 to both sides: x/2 = 10. Multiply by 2: x = 20. The solution is x = 20.
Math Problem 66: A rectangle’s length is twice its width. If the perimeter is 30 cm, what are the dimensions of the rectangle?
✨Solution: Let the width be w. Then the length is 2w. The perimeter is 2(w + 2w) = 30. Simplify: 6w = 30, so w = 5. The width is 5 cm, and the length is 10 cm.
Math Problem 67: Solve for x: 2(x − 4) = 10
✨Solution: Distribute: 2x − 8 = 10. Add 8: 2x = 18. Divide by 2: x = 9. The solution is x = 9.
Math Problem 68: If 3x − 7 = 2x + 5, what is x?
✨Solution: Subtract 2x from both sides: x − 7 = 5. Add 7: x = 12. The solution is x = 12.
Math Problem 69: A car travels at a constant speed. If it covers 60 miles in 2 hours, how far will it travel in t hours?
✨Solution: The speed is 60/2 = 30 miles per hour. In t hours, the distance is 30t miles. The formula is d = 30t.
Math Problem 70: Solve for x: 4x + 3 = 2x + 11
✨Solution: Subtract 2x from both sides: 2x + 3 = 11. Subtract 3: 2x = 8. Divide by 2: x = 4. The solution is x = 4.
Data Analysis & Probability (Math Word Problems 71-80)
Best for: Interpreting data and predicting outcomes.
Grades: 6–8
Math Problem 71: The scores on a test are: 85, 90, 78, 92, and 88. What is the mean score?
✨Solution: Add the scores: 85 + 90 + 78 + 92 + 88 = 433. Divide by the number of scores: 433 ÷ 5 = 86.6. The mean score is 86.6.
Math Problem 72: A spinner has 4 equal sections labeled 1, 2, 3, and 4. What is the probability of landing on an even number?
✨Solution: There are 2 even numbers (2 and 4) out of 4 total sections. The probability is 2/4 = 1/2. The probability is 1/2.
Math Problem 73: A survey shows that 12 out of 30 students prefer chocolate ice cream. What percentage of students prefer chocolate?
✨Solution: Divide and multiply by 100: 12/30 × 100 = 40%. 40% of students prefer chocolate.
Math Problem 74: A set of numbers is: 5, 7, 7, 9, 10. What is the mode of the set?
✨Solution: The mode is the most frequent number. The number 7 appears twice, while others appear once. The mode is 7.
Math Problem 75: A jar contains 5 red marbles, 3 blue marbles, and 2 green marbles. If you pick one marble at random, what is the probability of picking a blue marble?
✨Solution: Total marbles: 5 + 3 + 2 = 10. Blue marbles: 3. The probability is 3/10. The probability is 3/10.
Math Problem 76: A basketball player makes 7 out of 10 free throws. What is the experimental probability of making a free throw?
✨Solution: Divide successful attempts by total attempts: 7/10 = 0.7. The probability is 0.7 or 70%.
Math Problem 77: The heights of 5 students are: 150 cm, 155 cm, 160 cm, 155 cm, and 165 cm. What is the median height?
✨Solution: Arrange the heights in order: 150, 155, 155, 160, 165. The middle value is 155 cm.
Math Problem 78: A bag contains 8 candies: 3 chocolates, 2 mints, and 3 gummies. If you pick one candy at random, what is the probability of not picking a mint?
✨Solution: Total candies: 8. Non-mint candies: 8 − 2 = 6. The probability is 6/8 = 3/4. The probability is 3/4.
Math Problem 79: A die is rolled. What is the probability of rolling a number greater than 4?
✨Solution: Numbers greater than 4: 5 and 6. There are 2 favorable outcomes out of 6 total outcomes. The probability is 2/6 = 1/3. The probability is 1/3.
Math Problem 80: A bar graph shows the number of books read by students: 5, 7, 3, 8, and 6. What is the range of the data?
✨Solution: The range is the difference between the highest and lowest values: 8 − 3 = 5. The range is 5.
Advanced Problem Solving (Math Word Problems 81-90)
Best for: Tackling multi-step problems and higher-order thinking.
Grades: 6–12
Math Problem 81: A train travels 300 miles in 5 hours. If it continues at the same speed, how long will it take to travel 450 miles?
✨Solution: Find the speed: 300 ÷ 5 = 60 miles per hour. Time for 450 miles: 450 ÷ 60 = 7.5 hours. The time is 7.5 hours.
Math Problem 82: A rectangular field has an area of 200 square meters. If the length is 5 meters more than the width, what are the dimensions of the field?
✨Solution: Let the width be w. Then the length is w + 5. The area is w(w + 5) = 200. Expand: w² + 5w − 200 = 0. Factor: (w − 10)(w + 20) = 0. w = 10 (width). Length: w + 5 = 15. Dimensions: 10 m × 15 m.
Math Problem 83: A population of bacteria doubles every hour. If there are 100 bacteria initially, how many will there be after 5 hours?
✨Solution: Use the formula P = P₀ × 2ⁿ, where P₀ = 100 and n = 5. P = 100 × 2⁵ = 100 × 32 = 3200. The population is 3200 bacteria.
Math Problem 84: A store sells shirts for 20 each and pants for 30 each. If you buy 3 shirts and 2 pairs of pants, how much do you spend?
✨Solution: Cost of shirts: 3 × 20 = 60. Cost of pants: 2 × 30 = 60. Total cost: 60 + 60 = 120. You spend $120.
Math Problem 85: A right triangle has legs measuring 6 cm and 8 cm. What is the length of the hypotenuse?
✨Solution: Use the Pythagorean theorem: c² = a² + b². c² = 6² + 8² = 36 + 64 = 100. c = √100 = 10. The hypotenuse is 10 cm.
Math Problem 86: A car rental company charges 50 per day plus 0.20 per mile. If you rent the car for 3 days and drive 150 miles, how much will you pay?
✨Solution: Daily charge: 3 × 50 = 150. Mileage charge: 150 × 0.20 = 30. Total cost: 150 + 30 = 180. You will pay $180.
Math Problem 87: A recipe calls for 2 cups of flour to make 12 cookies. How many cups of flour are needed to make 108 cookies?
✨Solution: Set up a proportion: 2/12 = x/108. Solve for x: x = 2 × 108 ÷ 12 = 18. You need 18 cups of flour.
Math Problem 88: A cylindrical tank has a radius of 3 meters and a height of 10 meters. What is the volume of the tank?
✨Solution: Use the formula V = πr²h. V = π(3)²(10) = π(9)(10) = 90π. The volume is 90π cubic meters.
Math Problem 89: A school needs to transport 120 students using buses that hold 40 students each. How many buses are needed?
✨Solution: Divide the total students by the capacity of each bus: 120 ÷ 40 = 3. You need 3 buses.
Math Problem 90: A farmer wants to fence a rectangular field with an area of 100 square meters. If the length is 10 meters, what is the perimeter of the field?
✨Solution: Area: length × width = 100. Width: 100 ÷ 10 = 10. Perimeter: 2(length + width) = 2(10 + 10) = 40. The perimeter is 40 meters.
Mathematical Modeling (Math Word Problems 91-100)
Best for: Using math to create models and solve complex, multi-step problems.
Grades: 7–12
Math Problem 91: A population of rabbits doubles every year. If there are 50 rabbits initially, how many will there be after 4 years?
✨Solution: Use the formula P = P₀ × 2ⁿ, where P₀ = 50 and n = 4. P = 50 × 2⁴ = 50 × 16 = 800. There will be 800 rabbits.
Math Problem 92: A company sells widgets for 15 each. The cost to produce each widget is 8. How many widgets must they sell to make a profit of 700?
✨Solution: Profit per widget: 15 − 8 = 7. Number of widgets: 700 ÷ 7 = 100. They must sell 100 widgets.
Math Problem 93: A cylindrical tank has a radius of 4 meters and a height of 10 meters. How much water can it hold? (Use π ≈ 3.14.)
✨Solution: Volume: V = πr²h = 3.14 × (4)² × 10 = 3.14 × 16 × 10 = 502.4. The tank holds 502.4 cubic meters of water.
Math Problem 94: A car depreciates by 15% each year. If the car is worth 20,000 initially, what will its value be after 3 years?
✨Solution: Use the formula V = P(1 − r)ⁿ, where P = 20,000, r = 0.15, and n = 3. V = 20,000(1 − 0.15)³ = 20,000(0.85)³ = 20,000 × 0.614 = 12,280. The value is 12,280.
Math Problem 95: A rectangular field has an area of 300 square meters. If the length is twice the width, what are the dimensions of the field?
✨Solution: Let the width be w. Then the length is 2w. Area: w(2w) = 300. 2w² = 300. w² = 150. w = √150 ≈ 12.25. Width: 12.25 m, Length: 2w ≈ 24.5 m.
Math Problem 96: A bank account earns 5% interest compounded annually. If you deposit 1,000, how much will the account be worth after 2 years?
✨Solution: Use the formula A = P(1 + r)ⁿ, where P = 1000, r = 0.05, and n = 2. A = 1000(1 + 0.05)² = 1000(1.05)² = 1000 × 1.1025 = 1102.50. The account will be worth 1102.50.
Math Problem 97: A factory produces 200 units per hour. If production increases by 10% each hour, how many units will be produced in 3 hours?
✨Solution: Hour 1: 200. Hour 2: 200 × 1.10 = 220. Hour 3: 220 × 1.10 = 242. Total: 200 + 220 + 242 = 662 units.
Math Problem 98: A rocket launches vertically at 50 meters per second. If gravity slows it at 10 meters per second squared, how high will it go before stopping?
✨Solution: Use the formula v² = u² − 2a**s, where v = 0, u = 50, and a = 10. 0 = 50² − 2(10)s. s = 2500 ÷ 20 = 125. The rocket reaches 125 meters.
Math Problem 99: A group of friends shares a meal costing 120. If they split the bill equally and leave a 20 tip, how much does each person pay?
✨Solution: Total bill: 120 + 24 = 144. Each person pays: 144 ÷ 6 = 24. Each person pays 24.
Math Problem 100: A box contains 100 chocolates. If 20% are caramel-filled and 30% are nut-filled, how many are plain chocolates?
✨Solution: Caramel: 100 × 0.20 = 20. Nut-filled: 100 × 0.30 = 30. Plain: 100 − 20 − 30 = 50. There are 50 plain chocolates.
Critical Thinking Puzzles (Math Word Problems 101-110)
Best for: Stretching logical reasoning and problem-solving skills with non-traditional challenges.
Grades: 7–12
Math Problem 101: A man has a wolf, a goat, and a cabbage. He needs to cross a river with a boat that can carry only him and one item at a time. If left alone, the wolf will eat the goat, and the goat will eat the cabbage. How can he get everything across safely?
✨Solution: Take the goat first, then return and take the wolf. Leave the wolf and bring the goat back. Take the cabbage across, then return for the goat. Everything is transported safely.
Math Problem 102: You have two jugs: one holds 5 gallons, and the other holds 3 gallons. How can you measure exactly 4 gallons of water?
✨Solution: Fill the 5-gallon jug and pour into the 3-gallon jug until full. This leaves 2 gallons in the 5-gallon jug. Empty the 3-gallon jug, pour the 2 gallons into it, then fill the 5-gallon jug again and pour into the 3-gallon jug until full. You’ll have exactly 4 gallons in the 5-gallon jug.
Math Problem 103: Three friends check into a hotel room that costs 30. They each pay 10. Later, the clerk realizes the room was only 25 and gives 5 to the bellboy to return. The bellboy keeps 2 as a tip and gives 1 back to each friend. Now, each friend paid 9 (totaling 27) and the bellboy kept 2. Where did the extra dollar go?
✨Solution: There is no missing dollar. The 27 includes the 25 for the room and the 2 tip. The puzzle misleads by adding unrelated amounts.
Math Problem 104: A clock chimes once at 1:00, twice at 2:00, and so on. How many total chimes will it make in 12 hours?
✨Solution: Sum all the numbers from 1 to 12: 1 + 2 + 3 + ⋯ + 12 = 12 × (12 + 1) ÷ 2 = 78. The clock will chime 78 times.
Math Problem 105: A snail climbs up a 10-meter wall during the day but slides down 3 meters at night. How many days will it take to reach the top?
✨Solution: Each day, the net gain is 10 − 3 = 7 meters. On the 7th day, the snail climbs out without sliding back. It takes 7 days.
Math Problem 106: Five people are sitting at a round table. How many different ways can they arrange themselves?
✨Solution: For a round table, fix one person and arrange the others: (5 − 1)! = 4! = 24. There are 24 arrangements.
Math Problem 107: A frog jumps 3 feet forward but slides back 1 foot each time. How many jumps does it take to reach a pond 10 feet away?
✨Solution: Each jump gains 3 − 1 = 2 feet. After 4 jumps, the frog is at 8 feet. The fifth jump takes it to 10 feet. It takes 5 jumps.
Math Problem 108: A farmer has chickens and cows. If there are 20 heads and 56 legs, how many chickens and cows are there?
✨Solution: Let c be chickens and k be cows. Heads: c + k = 20. Legs: 2c + 4k = 56. Solve: c = 12, k = 8. There are 12 chickens and 8 cows.
Math Problem 109: A ladder has 15 rungs. If you start on the first rung and climb up 3 rungs, then down 2 rungs repeatedly, how many steps will it take to reach the top?
✨Solution: Each cycle (up 3, down 2) moves 1 rung higher. After 12 cycles, you’re on the 13th rung. One more step takes you to the top. It takes 13 steps.
Math Problem 110: A father is 30 years older than his son. In 5 years, the father will be twice as old as the son. How old are they now?
✨Solution: Let the son’s age be x. The father’s age is x + 30. In 5 years: x + 35 = 2(x + 5). Solve: x = 25. The son is 25, and the father is 55.
Fun & Creative Challenges (Math Word Problems 111-120)
Best for: Engaging students of all ages with non-traditional, open-ended problems.
Grades: All
Math Problem 111: You have 12 toothpicks arranged to form 4 squares. How can you move 3 toothpicks to create 3 squares instead?
✨Solution: Rearrange the toothpicks to form a large square with 3 smaller squares inside.
Math Problem 112: A magic square is a grid where the sums of each row, column, and diagonal are equal. Create a 3×3 magic square using the numbers 1 through 9.
✨Solution: Arrange the numbers as follows:
8 1 6
3 5 7
4 9 2
Each row, column, and diagonal sums to 15.
Math Problem 113: A baker has 3 loaves of bread. How can she divide them among 4 customers so each gets an equal share without wasting any bread?
✨Solution: Cut each loaf into 4 equal parts. Each customer gets 3 parts (3/4 of a loaf).
Math Problem 114: A frog lays eggs in a pond. Each egg becomes a tadpole, and each tadpole becomes a frog. If the number of frogs doubles every month, how many frogs will there be after 6 months if there is 1 frog initially?
✨Solution: Use the formula P = P₀ × 2ⁿ, where P₀ = 1 and n = 6. P = 1 × 2⁶ = 64. There will be 64 frogs.
Math Problem 115: A jar contains 10 red marbles and 5 blue marbles. If you randomly pick one marble, what is the probability of picking a red marble?
✨Solution: Total marbles: 10 + 5 = 15. Red marbles: 10. Probability: 10/15 = 2/3. The probability is 2/3.
Math Problem 116: A farmer wants to plant trees in rows. If each row must have 5 trees and the farmer has 23 trees, how many rows can he plant, and how many trees will be left over?
✨Solution: Divide: 23 ÷ 5 = 4 rows with a remainder of 3. He can plant 4 rows with 3 trees left over.
Math Problem 117: A clock shows 3:15. What is the angle between the hour and minute hands?
✨Solution: At 3:15, the minute hand is at 3 (15 minutes). The hour hand moves 1/4 of the way between 3 and 4. Each hour represents 30°, so 1/4 × 30 = 7.5°. The angle is 7.5°.
Math Problem 118: A treasure chest contains gold coins. If you divide the coins equally among 5 pirates, 3 coins are left over. If divided among 6 pirates, 4 coins are left over. What is the smallest number of coins in the chest?
✨Solution: Find the least common solution: x ≡ 3 mod 5 and x ≡ 4 mod 6. Trial and error gives x = 28. There are 28 coins.
Math Problem 119: A teacher writes numbers on the board: 1, 2, 3, …, 100. How many times does the digit 7 appear?
✨Solution: Count occurrences: 7 appears 10 times in the tens place (70–79) and 10 times in the ones place (7, 17, …, 97). Total: 10 + 10 = 20. The digit 7 appears 20 times.
Math Problem 120: A pizza is cut into 8 slices. If you eat half of the pizza and give away 2 slices, how many slices are left?
✨Solution: Half of 8 is 4 slices. Eat 4 and give away 2: 8 − 4 − 2 = 2. There are 2 slices left.
